零、前言

1.canvas本身提供了很多绘制基本图形的方法，普通绘制基本满足 2.但是更高级的绘制canvas便束手无策，但它的一个方法却将图形的绘制连接到了另一个次元 3.下面进入Path的世界，[注]:本文只说Path，关于绘制只要使用Canvas.drawPath(Path,Paint)即可 4.本文将对Path的所有API进行测试。

一、引：认识Path

例1.绘制网格

在Canvas篇我用Path画过一个网格辅助，在这里分析一下 moveTo相当于抬笔到某点，lineTo表示画下到某点

    /**
     * 绘制网格:注意只有用path才能绘制虚线
     *
     * @param step    小正方形边长
     * @param winSize 屏幕尺寸
     */
    public static Path gridPath(int step, Point winSize) {
        //创建path
        Path path = new Path();
        //每间隔step,将笔点移到(0, step * i)，然后画线到(winSize.x, step * i)
        for (int i = 0; i < winSize.y / step + 1; i++) {
            path.moveTo(0, step * i);
            path.lineTo(winSize.x, step * i);
        }

        for (int i = 0; i < winSize.x / step + 1; i++) {
            path.moveTo(step * i, 0);
            path.lineTo(step * i, winSize.y);
        }
        return path;
    }
//准备画笔
mRedPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mRedPaint.setColor(Color.RED);
mRedPaint.setStrokeWidth(2);
mRedPaint.setStyle(Paint.Style.STROKE);
//设置虚线效果new float[]{可见长度, 不可见长度},偏移值
mRedPaint.setPathEffect(new DashPathEffect(new float[]{10, 5}, 0)); 

//绘制
Path path = HelpPath.gridPath(50, mWinSize);
canvas.drawPath(path, mRedPaint);

例2.绘制N角星

曾经花了半天研究五角星的构造，通过两个圆，发现了N角星绘制的通法 又用半天用JavaScript的Canvas实现了在浏览器上的绘制，当然Android也不示弱：

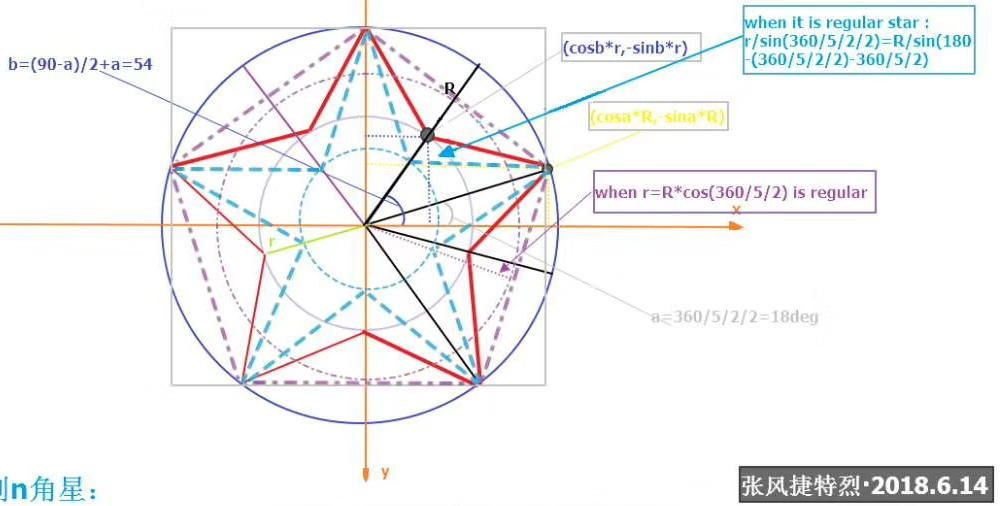
1).通用n角星路径绘制:(基本上都是一些点位和角度的计算，然后连线)

/**
 * n角星路径
 *
 * @param num 几角星
 * @param R   外接圆半径
 * @param r   内接圆半径
 * @return n角星路径
 */
public static Path nStarPath(int num, float R, float r) {
    Path path = new Path();
    float perDeg = 360 / num;
    float degA = perDeg / 2 / 2;
    float degB = 360 / (num - 1) / 2 - degA / 2 + degA;
    path.moveTo(
            (float) (Math.cos(rad(degA + perDeg * 0)) * R + R * Math.cos(rad(degA))),
            (float) (-Math.sin(rad(degA + perDeg * 0)) * R + R));
    for (int i = 0; i < num; i++) {
        path.lineTo(
                (float) (Math.cos(rad(degA + perDeg * i)) * R + R * Math.cos(rad(degA))),
                (float) (-Math.sin(rad(degA + perDeg * i)) * R + R));
        path.lineTo(
                (float) (Math.cos(rad(degB + perDeg * i)) * r + R * Math.cos(rad(degA))),
                (float) (-Math.sin(rad(degB + perDeg * i)) * r + R));
    }
    path.close();
    return path;
}   

/**
 * 角度制化为弧度制
 *
 * @param deg 角度
 * @return 弧度
 */
public static float rad(float deg) {
    return (float) (deg * Math.PI / 180);
}

2).当外接圆和内切圆的半径成一定的关系，可形成正多角星，和正多边形

正多角星:

    /**
     * 画正n角星的路径:
     *
     * @param num 角数
     * @param R   外接圆半径
     * @return 画正n角星的路径
     */
    public static Path regularStarPath(int num, float R) {
        float degA, degB;
        if (num % 2 == 1) {//奇数和偶数角区别对待
            degA = 360 / num / 2 / 2;
            degB = 180 - degA - 360 / num / 2;
        } else {
            degA = 360 / num / 2;
            degB = 180 - degA - 360 / num / 2;
        }
        float r = (float) (R * Math.sin(rad(degA)) / Math.sin(rad(degB)));
        return nStarPath(num, R, r);
    }

正多边形：

    /**
     * 画正n边形的路径
     *
     * @param num 边数
     * @param R   外接圆半径
     * @return 画正n边形的路径
     */
    public static Path regularPolygonPath(int num, float R) {
        float r = (float) (R * (Math.cos(rad(360 / num / 2))));//!!一点解决
        return nStarPath(num, R, r);
    }

    /**
     * 角度制化为弧度制
     *
     * @param deg 角度
     * @return 弧度
     */
    public static float rad(float deg) {
        return (float) (deg * Math.PI / 180);
    }

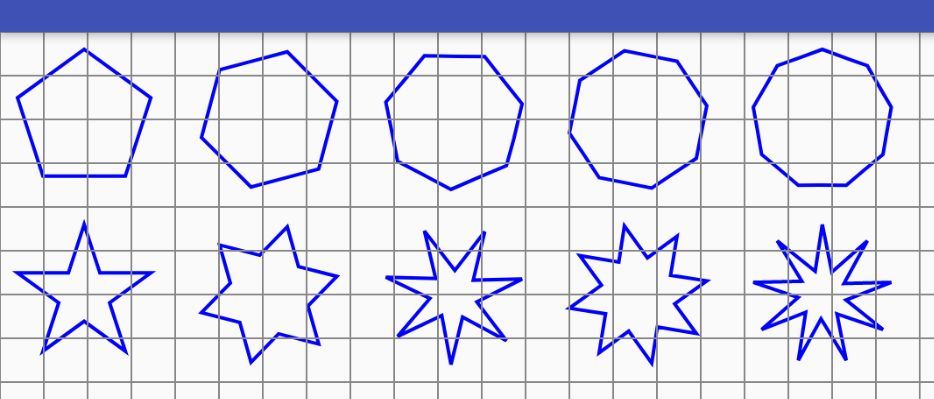
这两个小栗子作为引，应该对Path的能为有一定的了解了吧,下面将正式对Path做系统地介绍

二、Path的详细介绍

Path定位： 是一个类，直接继承自Object，源码行数879(一盏茶的功夫就看完了)，算个小类 但native方法很多，说明它跟底层打交道的，感觉不好惹 下面看一下Path的公共方法：(基本创建相关、添加相关、设置相关，其他) 注：为了好看，以下所有演示为横屏且canvas的坐标原点移至(800,500),所有蓝线为辅助线

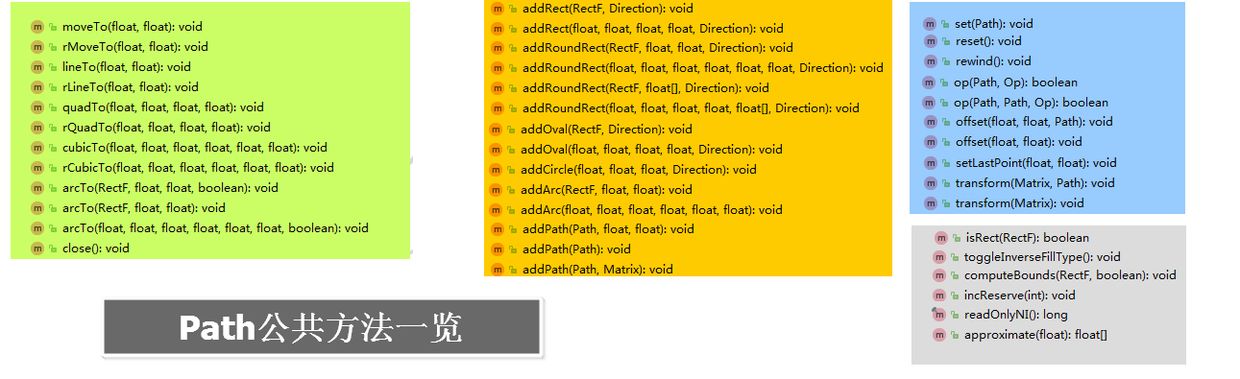
1.moveTo----lineTo----close

moveTo：抬笔到某点 lineTo：画线到某点 close：闭合首位

Path path = new Path();
path.moveTo(0, 0);
path.lineTo(100, 200);

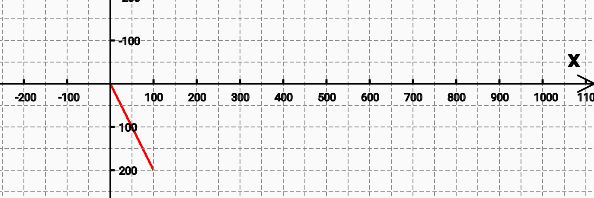
Path path = new Path();
path.moveTo(0, 0);
path.lineTo(100, 200);
path.lineTo(200, 100);

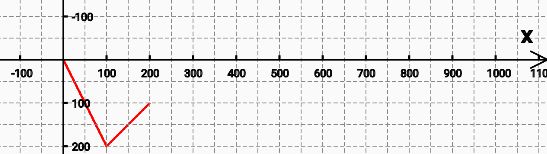
Path path = new Path();
path.moveTo(0, 0);
path.lineTo(100, 200);
path.lineTo(200, 100);
path.close();

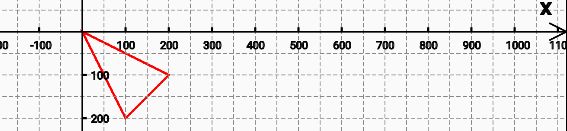
2.rMoveTo----rLineTo

rMoveTo：从路径尾部为起点，抬笔 rLineTo：从路径尾部为起点，画直线 其实也不难理解，就是点的参考系从canvas左上角移变成路径尾部，看一下就知道了：

Path path = new Path();
path.rMoveTo(0,0);
path.rLineTo(100, 200);
path.rLineTo(200, 100);
path.close();

3.绘制弧：arcTo(矩形范围，起点，终点，)

RectF rectF = new RectF(100, 100, 500, 300);
path.moveTo(0, 0);
//arcTo(矩形范围，起点，终点，是否独立--默认false)
//path.arcTo(rectF, 0, 45, true);
path.arcTo(rectF, 0, 45, false);

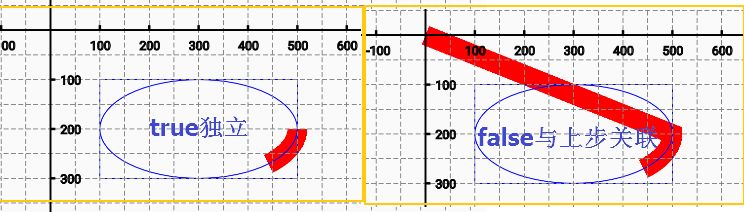
剩下的贝塞尔曲线这个大头放在本篇最后

三、路径添加：addXXX

可以看出齐刷刷的Direction，先看看它是什么鬼： 是一个枚举，只有CW(顺时针)和CCW(逆时针)，这里暂且按下，都使用CW,后文详述：

    public enum Direction {
        /** clockwise */
        CW  (0),    // must match enum in SkPath.h---顺时针
        /** counter-clockwise */
        CCW (1);    // must match enum in SkPath.h---逆时针

        Direction(int ni) {
            nativeInt = ni;
        }
        final int nativeInt;
    }

1.加矩形路径：

1).普通矩形:addRect(左,上,右,下)

RectF rectF = new RectF(100, 100, 500, 300);
path.addRect(rectF, Path.Direction.CW);//顺时针画矩形

2).圆角矩形：addRoundRect(矩形域,圆角x，圆角y)

RectF rectF = new RectF(100, 100, 500, 300);
path.addRoundRect(rectF, 50, 50, Path.Direction.CW);//顺时针画圆角矩形

3).用4点控制圆角：addRoundRect(矩形域,8数，方向)

RectF rectF = new RectF(100, 100, 500, 300);
path.addRoundRect(rectF, new float[]{
        150, 150,//左上圆角x,y
        0, 0,//右上圆角x,y
        450, 250,//右下圆角x,y
        250, 200//左下圆角x,y
}, Path.Direction.CW);//顺时针画

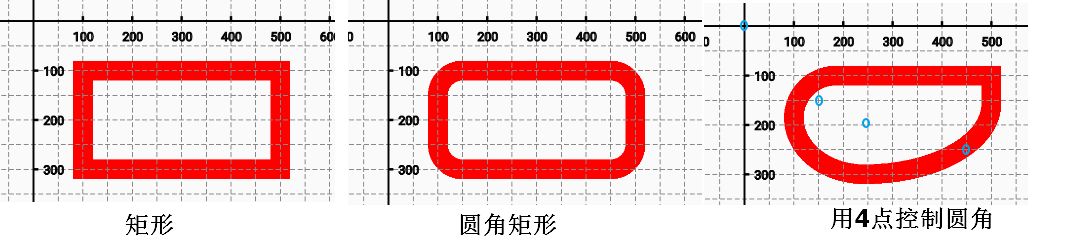
2.加椭圆路径：addOval(矩形域，方向)

RectF rectF = new RectF(100, 100, 500, 300);
path.addOval(rectF, Path.Direction.CW);

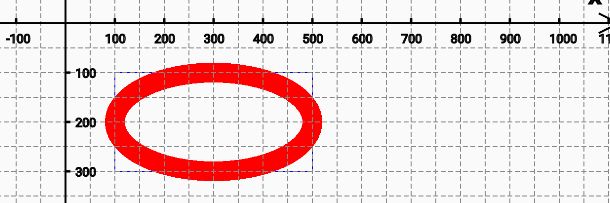
3.加圆路径：addCircle(圆心x,圆心y,方向)

path.addCircle(100,100,100,Path.Direction.CW);

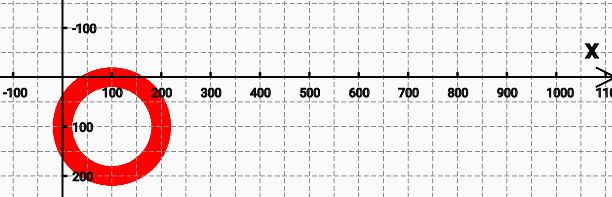
4.加弧线路径：addArc(矩形域,起始角度终止角度)

RectF rectF = new RectF(100, 100, 500, 300);
path.addArc(rectF,0,145);

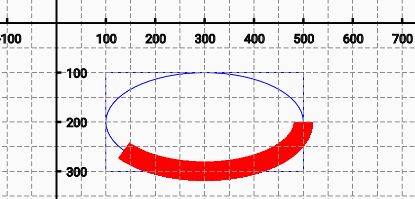
5.添加路径：

1).普通添加addPath(Path)

path.addCircle(100,100,100,Path.Direction.CW);
Path otherPath = new Path();
otherPath.moveTo(0, 0);
otherPath.lineTo(100, 100);
path.addPath(otherPath);

2).偏移添加：addPath(Path，偏移x,偏移y)

path.addCircle(100,100,100,Path.Direction.CW);
Path otherPath = new Path();
otherPath.moveTo(0, 0);
otherPath.lineTo(100, 100);
path.addPath(otherPath,200,200);

3).矩阵变换添加：addPath(Path，Matrix)

path.addCircle(100,100,100,Path.Direction.CW);
Path otherPath = new Path();
otherPath.moveTo(0, 0);
otherPath.lineTo(100, 100);

Matrix matrix = new Matrix();
matrix.setValues(new float[]{
        1, 0, 100,
        0, .5f, 150,
        0, 0, 1
});
path.addPath(otherPath, matrix);

四、其他操作：

1.细碎小点综述:

        path.reset();//清空path,保留填充类型
        //path.rewind();//清空path,保留数据结构
        path.isEmpty()//是否为空
        path.isRect(new RectF());
        path.isConvex();
        path.isInverseFillType();

        path.set(otherPath);//清空path后添加新Path
//        path.offset(200,200);//平移
//        path.transform(matrix);//矩阵变换

        Path tempPath = new Path();
//        path.offset(200, 200, tempPath);//基于path平移注入tempPath，path不变
        path.transform(matrix, tempPath);//基于path变换注入tempPath，path不变

        canvas.drawPath(path, mRedPaint);
        canvas.drawPath(tempPath, mRedPaint);

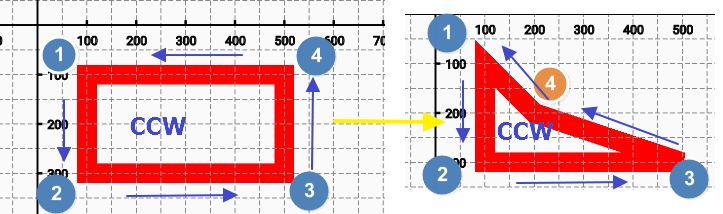
2.顺时针CW和逆时针CCW的区别

1).setLastPoint(x,y):设置最后一点

Path相当于将点按顺序保存，setLastPoint(x,y)方法则是将最后一个点换掉

RectF rectF = new RectF(100, 100, 500, 300);
path.addRect(rectF, Path.Direction.CW);//顺时针画矩形
path.setLastPoint(200, 200);
canvas.drawPath(path, mRedPaint);

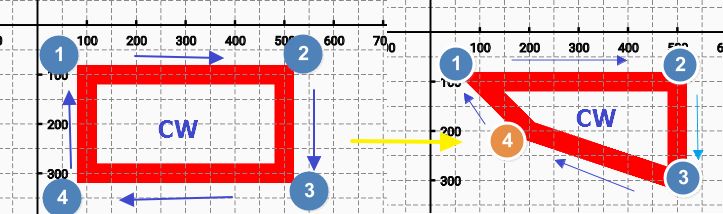
RectF rectF = new RectF(100, 100, 500, 300);
path.addRect(rectF, Path.Direction.CCW);//顺时针画矩形
path.setLastPoint(200, 200);
canvas.drawPath(path, mRedPaint);

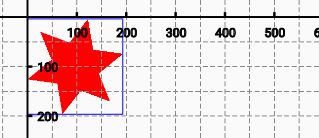
3.边界计算：

Path starPath = CommonPath.nStarPath(6, 100, 50);
RectF rectF = new RectF();//自备矩形区域
starPath.computeBounds(rectF, true);
canvas.drawPath(starPath, mRedPaint);
canvas.drawRect(rectF,mHelpPaint);

五、路径的填充

1.初识路径的填充：

1)左图：两个都是顺时针：

mRedPaint.setStyle(Paint.Style.FILL);
RectF rectF = new RectF(100, 100, 500, 300);
path.addRect(rectF, Path.Direction.CW);//顺时针画矩形
path.addRect(200, 0, 400, 400, Path.Direction.CW);//顺时针画矩形

2)右图：横的顺时针,竖的逆时针

mRedPaint.setStyle(Paint.Style.FILL);
RectF rectF = new RectF(100, 100, 500, 300);
path.addRect(rectF, Path.Direction.CW);//顺时针画矩形
path.addRect(200, 0, 400, 400, Path.Direction.CCW);//逆时针画矩形

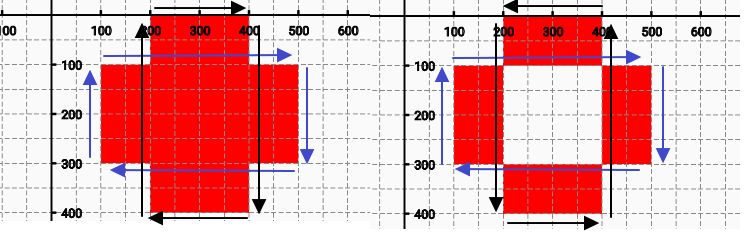
感觉向两个水涡，同向加剧，反向中间就抵消了

2.填充的环绕原则：---在自然科学(如数学，物理学)中的概念

非零环绕原则(WINDING)----默认 反零环绕原则(INVERSE_WINDING) 奇偶环绕原则(EVEN_ODD) 反奇偶环绕原则(INVERSE_EVEN_ODD)

  public enum FillType {
        WINDING         (0),
        EVEN_ODD        (1),
        INVERSE_WINDING (2),
        INVERSE_EVEN_ODD(3);
        FillType(int ni) {
            nativeInt = ni;
        }
        final int nativeInt;
    }
Path.FillType fillType = path.getFillType();//获取类型
path.setFillType(Path.FillType.XXXXXX)//设置类型
//绘制的测试五角星
path.moveTo(100, 200);
path.lineTo(500, 200);
path.lineTo(200, 400);
path.lineTo(300, 50);
path.lineTo(400, 400);
path.close();

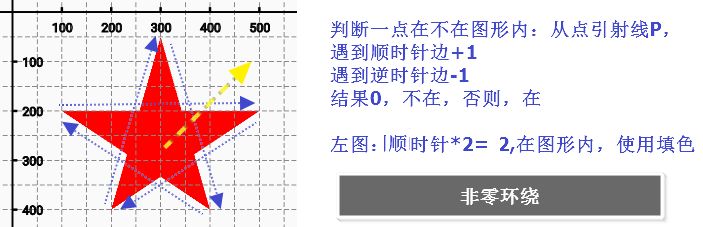
1).非零环绕数规则：WINDING

根据我个人的理解(仅供参考)：在非零环绕数规则下

判断一点在不在图形内：从点引射线P，
遇到顺时针边+1
遇到逆时针边-1
结果0，不在，否则，在

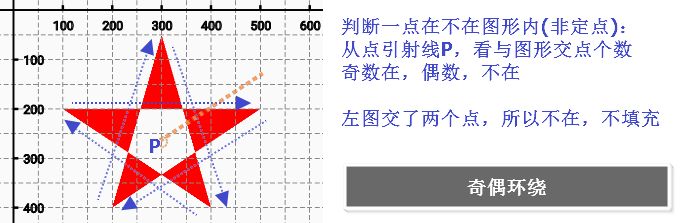
2).奇偶环绕数规则：EVEN_ODD

根据我个人的理解(仅供参考)：奇偶环绕数规则

判断一点在不在图形内(非定点)：
从点引射线P，看与图形交点个数
奇数在，偶数，不在

3).反非零环绕数规则和反奇偶环绕数规则：

就是和上面相比，该填充的不填充，不填充的填充

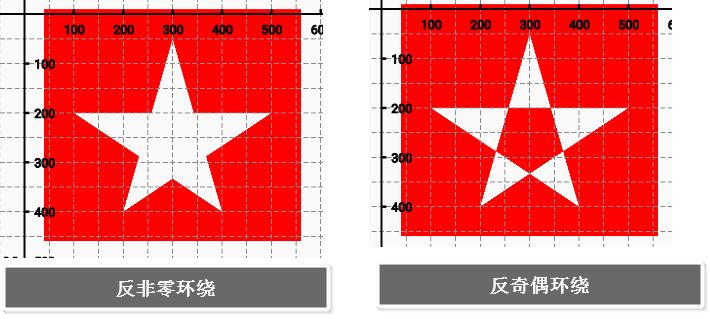
这样看来图形的顺时针或逆时针绘制对于填充是非常重要的 综合来说奇偶原则比较简单粗暴,但非零原则作为默认方式体现了它的通用性

六、布尔运算OP：(两个路径之间的运算)

如果说环绕原则是一个Path的自我纠结，那么OP就是两个路径之间的勾心斗角

Path right = new Path();
Path left = new Path();
left.addCircle(0, 0, 100, Path.Direction.CW);
right.addCircle(100, 0, 100, Path.Direction.CW);
//left.op(right, Path.Op.DIFFERENCE);//差集----晕，咬了一口硫酸
//left.op(right, Path.Op.REVERSE_DIFFERENCE);//反差集----赔了夫人又折兵
//left.op(right, Path.Op.INTERSECT);//交集----与你不同的都不是我
//left.op(right, Path.Op.UNION);//并集----在一起，在一起
left.op(right, Path.Op.XOR);//异或集---我恨你，我也恨你

canvas.drawPath(left, mRedPaint);

七、Path动画：PathMeasure

init方法里：

//测量路径
PathMeasure pathMeasure = new PathMeasure(mStarPath, false);
//使用ValueAnimator
ValueAnimator pathAnimator = ValueAnimator.ofFloat(1, 0);
pathAnimator.setDuration(5000);
pathAnimator.addUpdateListener(animation -> {
    float value = (Float) animation.getAnimatedValue();
    //使用画笔虚线效果+偏移
    DashPathEffect effect = new DashPathEffect(
            new float[]{pathMeasure.getLength(), pathMeasure.getLength()},
            value * pathMeasure.getLength());
    mRedPaint.setPathEffect(effect);
    invalidate();
});
pathAnimator.start();

OnDraw方法里：

canvas.drawPath(mStarPath, mRedPaint);

八、贝塞尔曲线简述：

如果说Path是Canvas为了高级绘制留下的窗子那么贝塞尔曲线则Path为了更高级的绘制而留下的门 由于操作的复杂性，这里并不过渡深入，以后有需求的话会专门开一篇

1.简单认识：(图来源网络)

2.二阶贝塞尔曲线示例：

public class Bezier2View extends View {
    private Paint mHelpPaint;//辅助画笔
    private Paint mPaint;//贝塞尔曲线画笔
    private Path mBezierPath;//贝塞尔曲线路径
    //起点
    private PointF start = new PointF(0, 0);
    //终点
    private PointF end = new PointF(400, 0);
    //控制点
    private PointF control = new PointF(200, 200);
    private Picture mPicture;//坐标系和网格的Canvas元件
    private Point mCoo;//坐标系
    public Bezier2View(Context context) {
        this(context, null);
    }

    public Bezier2View(Context context, @Nullable AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        //贝塞尔曲线画笔
        mPaint = new Paint();
        mPaint.setStyle(Paint.Style.STROKE);
        mPaint.setColor(Color.parseColor("#88EC17F3"));
        mPaint.setStrokeWidth(8);
        //辅助线画笔
        resetHelpPaint();
        recordBg();//初始化时录制坐标系和网格--避免在Ondraw里重复调用
        mBezierPath = new Path();
    }

    /**
     * 初始化时录制坐标系和网格--避免在Ondraw里重复调用
     */
    private void recordBg() {
        //准备屏幕尺寸
        Point winSize = new Point();
        mCoo = new Point(800, 500);
        Utils.loadWinSize(getContext(), winSize);
        Paint gridPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPicture = new Picture();
        Canvas recordCanvas = mPicture.beginRecording(winSize.x, winSize.y);
        //绘制辅助网格
        HelpDraw.drawGrid(recordCanvas, winSize, gridPaint);
        //绘制坐标系
        HelpDraw.drawCoo(recordCanvas, mCoo, winSize, gridPaint);
        mPicture.endRecording();
    }

    /**
     * 重置辅助画笔
     */
    private void resetHelpPaint() {
        mHelpPaint = new Paint();
        mHelpPaint.setColor(Color.BLUE);
        mHelpPaint.setStrokeWidth(2);
        mHelpPaint.setStyle(Paint.Style.STROKE);
        mHelpPaint.setPathEffect(new DashPathEffect(new float[]{10, 5}, 0));
        mHelpPaint.setStrokeCap(Paint.Cap.ROUND);
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        // 根据触摸位置更新控制点，并提示重绘
        control.x = event.getX() - mCoo.x;
        control.y = event.getY() - mCoo.y;
        invalidate();
        return true;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();
        canvas.translate(mCoo.x, mCoo.y);
        drawHelpElement(canvas);//绘制辅助工具--控制点和基准选
        // 绘制贝塞尔曲线
        mBezierPath.moveTo(start.x, start.y);
        mBezierPath.quadTo(control.x, control.y, end.x, end.y);
        canvas.drawPath(mBezierPath, mPaint);
        mBezierPath.reset();//清空mBezierPath
        canvas.restore();
        canvas.drawPicture(mPicture);
    }
    /**
     * 绘制辅助工具--控制点和基准选
     *
     * @param canvas
     */
    private void drawHelpElement(Canvas canvas) {
        // 绘制数据点和控制点
        mHelpPaint.setColor(Color.parseColor("#8820ECE2"));
        mHelpPaint.setStrokeWidth(20);
        canvas.drawPoint(start.x, start.y, mHelpPaint);
        canvas.drawPoint(end.x, end.y, mHelpPaint);
        canvas.drawPoint(control.x, control.y, mHelpPaint);
        // 绘制辅助线
        resetHelpPaint();
        canvas.drawLine(start.x, start.y, control.x, control.y, mHelpPaint);
        canvas.drawLine(end.x, end.y, control.x, control.y, mHelpPaint);
    }
}

效果如下：(模拟器+录屏软件+AS有点卡，手机上演示很流畅的)

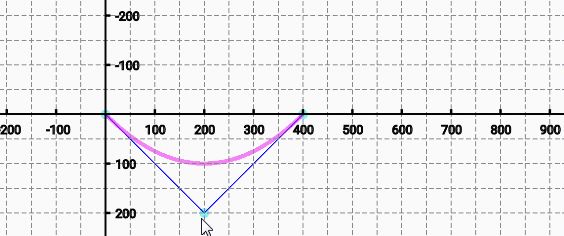
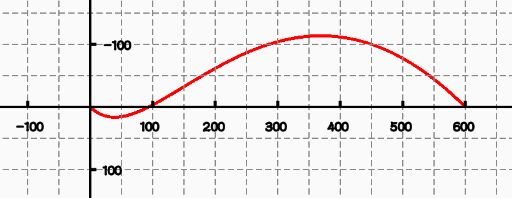
3.三阶贝塞尔的简单演示：

mRedPaint.setStrokeWidth(5);
mRedPaint.setStrokeCap(Paint.Cap.ROUND);
path.moveTo(0, 0);//定点1_x,定点1_y
//(控制点1_X，控制点1_y,控制点2_x，控制点2_y,定点2_x,定点2_y)
path.cubicTo(100, 100, 300, -300, 600, 0);

好了，Path完结散花

后记：捷文规范

1.本文成长记录及勘误表

2.声明

1----本文由张风捷特烈原创,转载请注明 2----欢迎广大编程爱好者共同交流 3----个人能力有限，如有不正之处欢迎大家批评指证，必定虚心改正 4----看到这里，我在此感谢你的喜欢与支持