二分搜索树节点的插入

一. 定义二分搜索树

首先定义一颗二分搜索树，C++代码如下：

#include <iostream>
#include <queue>
#include <cassert>
using namespace std;

//套用模板函数
template <typename Key, typename Value>
class BST {
  private://构造节点Node  
  struct Node 
  {
    Key key;
    Value value;
    Node *left;     //左孩子指针
    Node *right;    //右孩子指针

    Node(Key key, Value value) 
   {
     this->key = key;
     this->value = value;
      //初始值为空
     this->left = this->right = NULL;
    }
    Node(Node *node)
    {
        this->key = node->key;
        this->value = node->value;
        this->left = node->left;
      this->right = node->right;
  }
};

//根节点
Node *root;//节点数量 
int count;
  
public://构造函数
BST() 
{
    //初始值为空
    root = NULL;
    count = 0;
}

//析构函数~BST() {distroy(root);}

二. 插入节点

接下来我们开始对二分搜索树中进行插入节点，如图：

我们向树中插入键值为60的节点

1. 首先60会和整个数的根节点比较，显然60 > 41 所以将60，继续和41节点的右孩子进行比较：
2. 
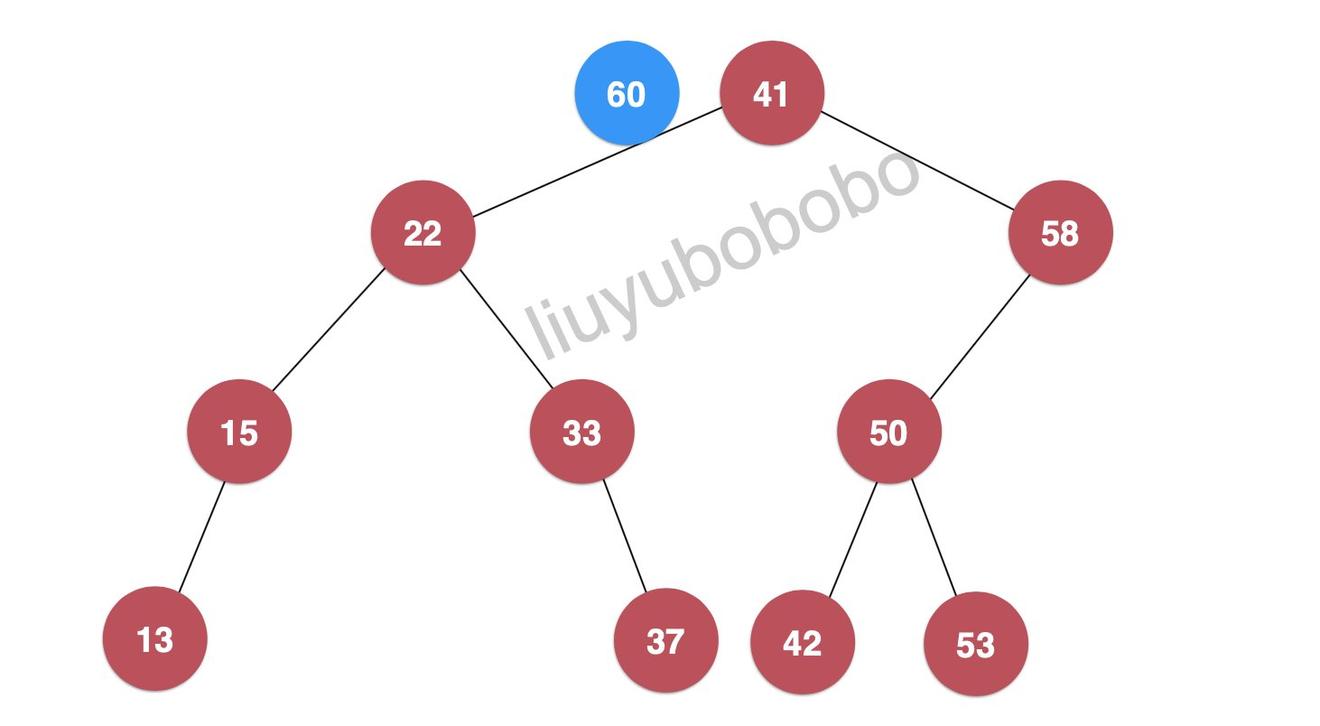
3. 此时 60 > 58 ，所以将60 继续和58节点的右孩子节点进行比较，但58节点的右孩子为空，这时 60 节点就插入为58节点的右孩子：
4. 

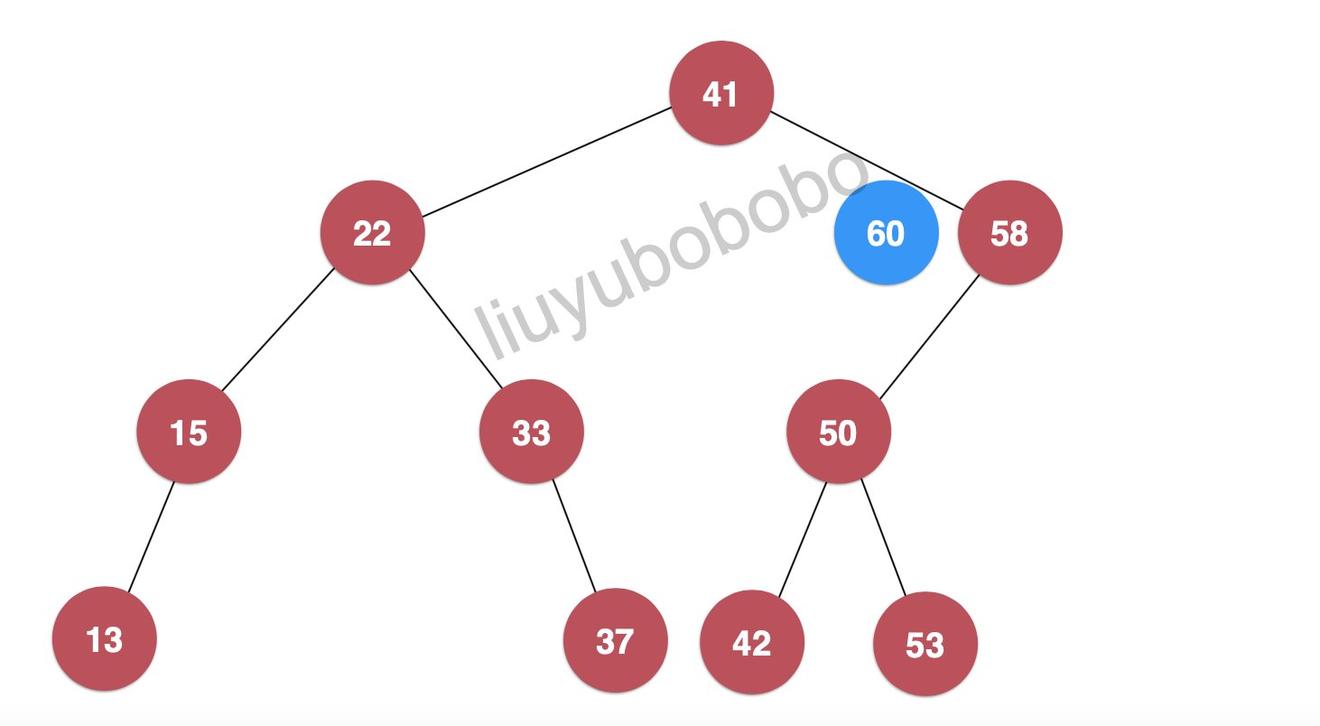
下面我们再向二分搜索树中插入键值为28的节点：

1. 节点28和二分搜索树的根节点41比较，28 < 41 ,将28继续和41节点的左孩子节点比较：
2. 
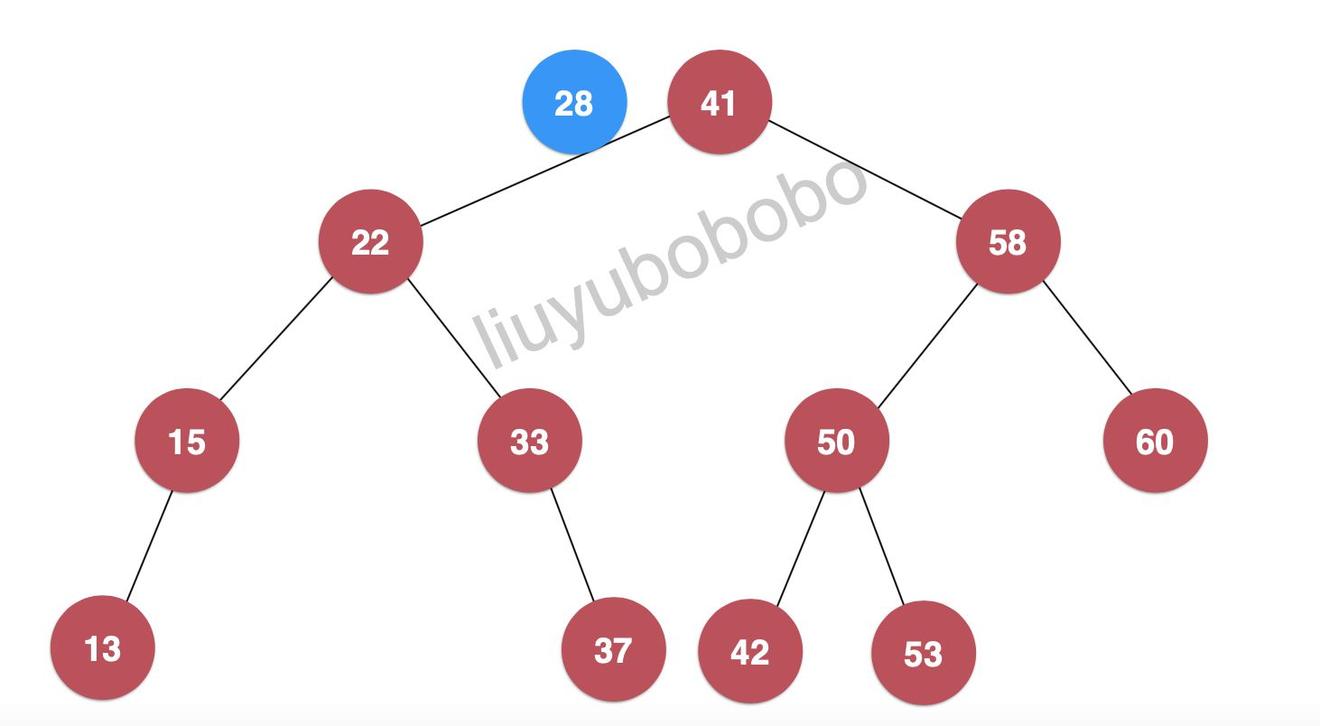
3. 此时28 > 22, 再将28和22节点的左孩子比较：
4. 
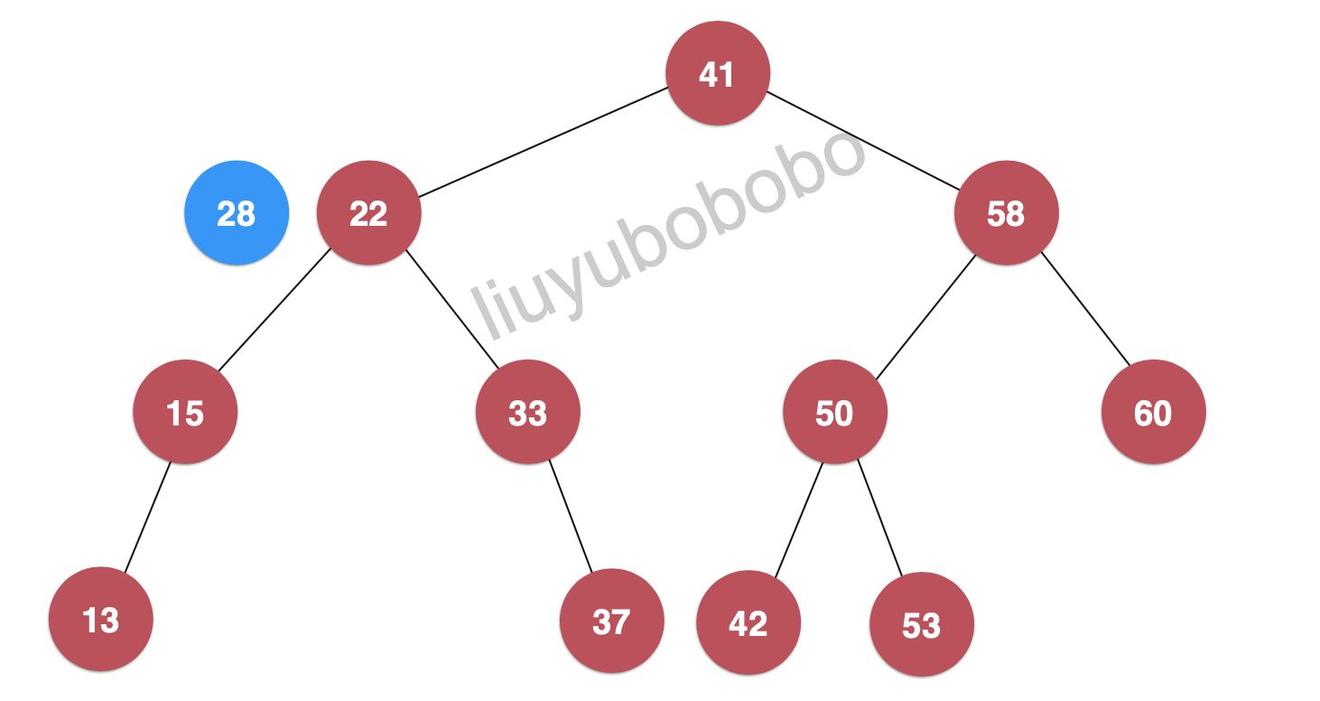
5. 28 < 33,继续将节点28和33节点的右孩子比较，但此时33的左孩子为空，28节点就插入为节点33的左孩子：
6. 

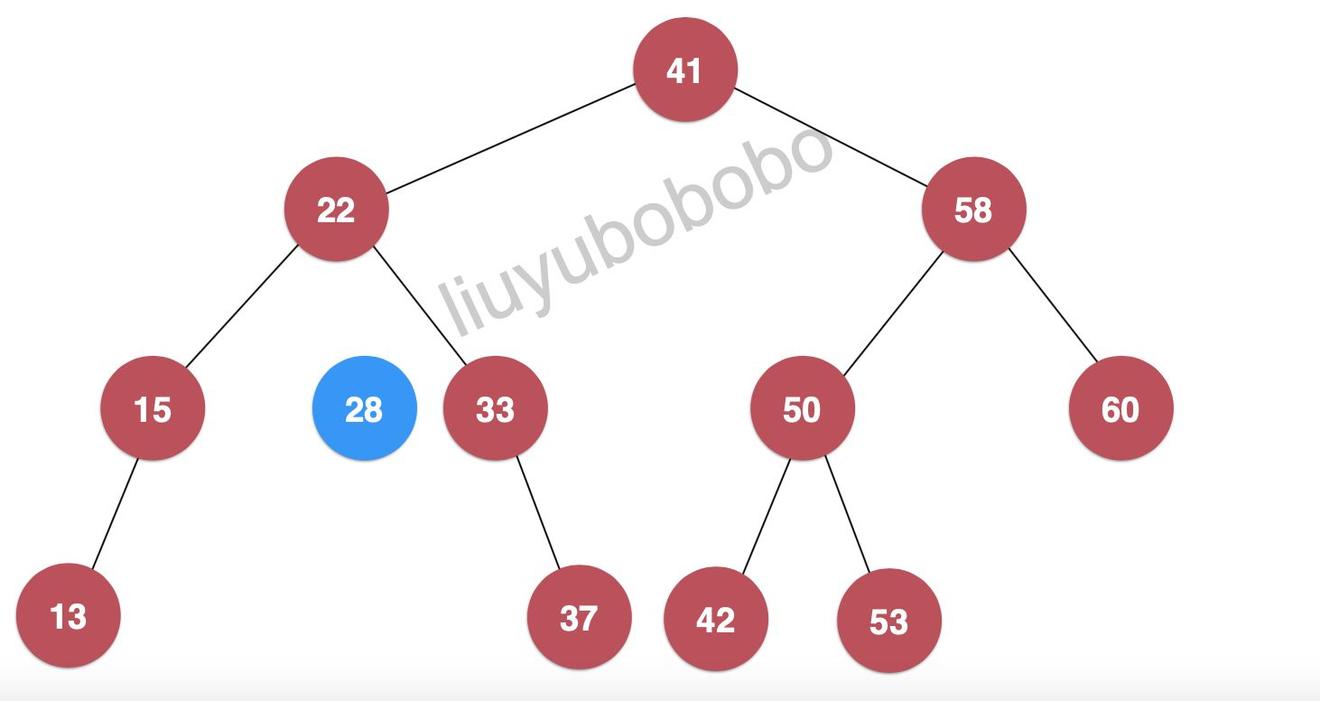
如果出现插入的节点和二分搜索树中的节点重合的情况，依然是同理，只需要将原来节点覆盖即可

三. 代码实现

新节点的插入操作的逻辑明白了，下面我们开始带着这种逻辑进入代码的实现(使用递归版本，c++实现）：

我们在public中定义函数：

//插入操作
void insert(Key key, Value value) 
{
  //向根节点中插入key， value
  root = insert(root, key, value);
}

接下来我们在private中写：

//插入操作
//向以node为根节点的二分搜索树中，插入节点（key，value),使用递归算法
//返回插入新节点后的二分搜索树的根
Node *insert(Node *node, Key key, Value value) 
{
  if (node == NULL) 
  {
     count++;
     return new Node(key, value);
  }

    if (key == node->key) 
    {
        node->value = value;
    } 
    else if (key > node->key) 
    {
        node->right = insert(node->right, key, value);
    } 
    else //key < node->key
       node->left = insert(node->left, key, value);
}